pyxu.abc#

pyxu.abc.operator #

class Property(value, names=<not given>, *values, module=None, qualname=None, type=None, start=1, boundary=None)[source]#

Bases: Enum

Mathematical property.

See also

Operator

CAN_EVAL = 1#

FUNCTIONAL = 2#

PROXIMABLE = 3#

DIFFERENTIABLE = 4#

DIFFERENTIABLE_FUNCTION = 5#

LINEAR = 6#

LINEAR_SQUARE = 7#

LINEAR_NORMAL = 8#

LINEAR_IDEMPOTENT = 9#

LINEAR_SELF_ADJOINT = 10#

LINEAR_POSITIVE_DEFINITE = 11#

LINEAR_UNITARY = 12#

QUADRATIC = 13#

arithmetic_methods()[source]#

Instance methods affected by arithmetic operations.

Return type:: Set[str]

class Operator(dim_shape, codim_shape)[source]#

Bases: object

Abstract Base Class for Pyxu operators.

Goals:

enable operator arithmetic.
cast operators to specialized forms.
attach Property tags encoding certain mathematical properties. Each core sub-class must have a unique set of properties to be distinguishable from its peers.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

__init__(dim_shape, codim_shape)[source]#

Parameters:

dim_shape (NDArrayShape) – (M1,…,MD) operator input shape.
codim_shape (NDArrayShape) – (N1,…,NK) operator output shape.

property dim_shape: Integral | tuple[Integral, ...]#: Return shape of operator’s domain. (M1,…,MD)

property dim_size: Integral#: Return size of operator’s domain. (M1*…*MD)

property dim_rank: Integral#: Return rank of operator’s domain. (D)

property codim_shape: Integral | tuple[Integral, ...]#: Return shape of operator’s co-domain. (N1,…,NK)

property codim_size: Integral#: Return size of operator’s co-domain. (N1*…*NK)

property codim_rank: Integral#: Return rank of operator’s co-domain. (K)

classmethod properties()[source]#

Mathematical properties of the operator.

Return type:: Set[Property]

classmethod has(prop)[source]#

Verify if operator possesses supplied properties.

Parameters:: prop (Property | Collection[Property])
Return type:: bool

asop(cast_to)[source]#

Recast an Operator (or subclass thereof) to another Operator.

Users may call this method if the arithmetic API yields sub-optimal return types.

This method is a no-op if cast_to is a parent class of self.

Parameters:

cast_to (OpC) – Target type for the recast.

Returns:

op – Operator with the new interface.

Fails when cast is forbidden. (Ex: Map -> Func if codim.size > 1)

Return type:

OpT

Notes

The interface of cast_to is provided via encapsulation + forwarding.
If self does not implement all methods from cast_to, then unimplemented methods will raise NotImplementedError when called.

__add__(other)[source]#

Add two operators.

Parameters:

self (OpT) – Left operand.
other (OpT) – Right operand.

Returns:

op – Composite operator self + other

Return type:

OpT

Notes

Operand shapes must be consistent, i.e.:

have same dimensions, and

have compatible co-dimensions (after broadcasting).

See also

AddRule

__sub__(other)[source]#

Subtract two operators.

Parameters:

self (OpT) – Left operand.
other (OpT) – Right operand.

Returns:

op – Composite operator self - other

Return type:

OpT

__neg__()[source]#

Negate an operator.

Returns:: op – Composite operator -1 * self.
Return type:: OpT

__mul__(other)[source]#

Compose two operators, or scale an operator by a constant.

Parameters:

self (OpT) – Left operand.
other (Real, OpT) – Scalar or right operand.

Returns:

op – Scaled operator or composed operator self * other.

Return type:

OpT

Notes

If called with two operators, their shapes must be consistent, i.e. self.dim_shape == other.codim_shape.

See also

ScaleRule, ChainRule

__pow__(k)[source]#

Parameters:: k (Integral)
Return type:: OpT

argscale(scalar)[source]#

Scale operator’s domain.

Parameters:: scalar (Real)
Returns:: op – Domain-scaled operator.
Return type:: OpT

See also

ArgScaleRule

argshift(shift)[source]#

Shift operator’s domain.

Parameters:

shift (NDArray) –

Shift value \(c \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\).

shift must be broadcastable with operator’s dimension.

Returns:

op – Domain-shifted operator \(g(x) = f(x + c)\).

Return type:

OpT

See also

ArgShiftRule

expr(level=0, strip=True)[source]#

Pretty-Print the expression representation of the operator.

Useful for debugging arithmetic-induced expressions.

Example

import numpy as np
import pyxu.abc as pxa

kwargs = dict(dim_shape=5, codim_shape=5)
op1 = pxa.LinOp(**kwargs)
op2 = pxa.DiffMap(**kwargs)
op = ((2 * op1) + (op1 * op2)).argshift(np.r_[1])

print(op.expr())
# [argshift, ==> DiffMap(dim=(5,), codim=(5,))
# .[add, ==> DiffMap(dim=(5,), codim=(5,))
# ..[scale, ==> LinOp(dim=(5,), codim=(5,))
# ...LinOp(dim=(5,), codim=(5,)),
# ...2.0],
# ..[compose, ==> DiffMap(dim=(5,), codim=(5,))
# ...LinOp(dim=(5,), codim=(5,)),
# ...DiffMap(dim=(5,), codim=(5,))]],
# .(1,)]

Parameters:

level (int)
strip (bool)

Return type:

str

squeeze(axes=None)[source]#

Drop size-1 axes from co-dimension.

See also

SqueezeAxes

Parameters:: axes (Integral | tuple[Integral, ...])
Return type:: OpT

transpose(axes=None)[source]#

Permute co-dimension axes.

See also

TransposeAxes

Parameters:: axes (Integral | tuple[Integral, ...])
Return type:: OpT

reshape(codim_shape)[source]#

Reshape co-dimension shape.

See also

ReshapeAxes

Parameters:: codim_shape (Integral | tuple[Integral, ...])
Return type:: OpT

broadcast_to(codim_shape)[source]#

Broadcast co-dimension shape.

See also

BroadcastAxes

Parameters:: codim_shape (Integral | tuple[Integral, ...])
Return type:: OpT

subsample(*indices)[source]#

Sub-sample co-dimension.

See also

SubSample

Return type:: OpT

rechunk(chunks)[source]#

Re-chunk core dimensions to new chunk size.

See also

RechunkAxes()

Parameters:: chunks (dict)
Return type:: OpT

class Map(dim_shape, codim_shape)[source]#

Bases: Operator

Base class for real-valued maps \(\mathbf{f}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\).

Instances of this class must implement apply().

If \(\mathbf{f}\) is Lipschitz-continuous with known Lipschitz constant \(L\), the latter should be stored in the lipschitz property.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

classmethod properties()[source]#

Mathematical properties of the operator.

Return type:: Set[Property]

apply(arr)[source]#

Evaluate operator at specified point(s).

Parameters:: arr (NDArray) – (…, M1,…,MD) input points.
Returns:: out – (…, N1,…,NK) output points.
Return type:: NDArray

__call__(arr)[source]#

Alias for apply().

Parameters:: arr (NDArray)
Return type:: NDArray

property lipschitz: Real#

Return the last computed Lipschitz constant of \(\mathbf{f}\).

Notes

If a Lipschitz constant is known apriori, it can be stored in the instance as follows:

class TestOp(Map):
    def __init__(self, dim_shape, codim_shape):
        super().__init__(dim_shape, codim_shape)
        self.lipschitz = 2

op = TestOp(2, 3)
op.lipschitz  # => 2

Alternatively the Lipschitz constant can be set manually after initialization:

class TestOp(Map):
    def __init__(self, dim_shape, codim_shape):
        super().__init__(dim_shape, codim_shape)

op = TestOp(2, 3)
op.lipschitz  # => inf, since unknown apriori

op.lipschitz = 2  # post-init specification
op.lipschitz  # => 2

lipschitz() never computes anything: call estimate_lipschitz() manually to compute a new Lipschitz estimate:
```
op.lipschitz = op.estimate_lipschitz()
```

estimate_lipschitz(**kwargs)[source]#

Compute a Lipschitz constant of the operator.

Parameters:: kwargs (Mapping) – Class-specific kwargs to configure Lipschitz estimation.
Return type:: Real

Notes

This method should always be callable without specifying any kwargs.
A constant \(L_{\mathbf{f}} > 0\) is said to be a Lipschitz constant for a map \(\mathbf{f}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\) if:

\[\|\mathbf{f}(\mathbf{x}) - \mathbf{f}(\mathbf{y})\|_{\mathbb{R}^{N_{1} \times\cdots\times N_{K}}} \leq L_{\mathbf{f}} \|\mathbf{x} - \mathbf{y}\|_{\mathbb{R}^{M_{1} \times\cdots\times M_{D}}}, \qquad \forall \mathbf{x}, \mathbf{y}\in \mathbb{R}^{M_{1} \times\cdots\times M_{D}},\]

where \(\|\cdot\|_{\mathbb{R}^{M_{1} \times\cdots\times M_{D}}}\) and \(\|\cdot\|_{\mathbb{R}^{N_{1} \times\cdots\times N_{K}}}\) are the canonical norms on their respective spaces.

The smallest Lipschitz constant of a map is called the optimal Lipschitz constant.

class Func(dim_shape, codim_shape)[source]#

Bases: Map

Base class for real-valued functionals \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}\cup\{+\infty\}\).

Instances of this class must implement apply().

If \(f\) is Lipschitz-continuous with known Lipschitz constant \(L\), the latter should be stored in the lipschitz property.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

class DiffMap(dim_shape, codim_shape)[source]#

Bases: Map

Base class for real-valued differentiable maps \(\mathbf{f}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\).

Instances of this class must implement apply() and jacobian().

If \(\mathbf{f}\) is Lipschitz-continuous with known Lipschitz constant \(L\), the latter should be stored in the lipschitz property.

If \(\mathbf{J}_{\mathbf{f}}\) is Lipschitz-continuous with known Lipschitz constant \(\partial L\), the latter should be stored in the diff_lipschitz property.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

jacobian(arr)[source]#

Evaluate the Jacobian of \(\mathbf{f}\) at the specified point.

Parameters:: arr (NDArray) – (M1,…,MD) evaluation point.
Returns:: op – Jacobian operator at point arr.
Return type:: OpT

Notes

Let \(\mathbf{f}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\) be a differentiable multi-dimensional map. The Jacobian (or differential) of \(\mathbf{f}\) at \(\mathbf{z} \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\) is defined as the best linear approximator of \(\mathbf{f}\) near \(\mathbf{z}\), in the following sense:

\[\mathbf{f}(\mathbf{x}) - \mathbf{f}(\mathbf{z}) = \mathbf{J}_{\mathbf{f}}(\mathbf{z}) (\mathbf{x} - \mathbf{z}) + o(\| \mathbf{x} - \mathbf{z} \|) \quad \text{as} \quad \mathbf{x} \to \mathbf{z}.\]

The Jacobian admits the following matrix representation:

\[[\mathbf{J}_{\mathbf{f}}(\mathbf{x})]_{ij} := \frac{\partial f_{i}}{\partial x_{j}}(\mathbf{x}), \qquad \forall (i,j) \in \{1,\ldots,N_{1}\cdots N_{K}\} \times \{1,\ldots,M_{1}\cdots M_{D}\}.\]

property diff_lipschitz: Real#

Return the last computed Lipschitz constant of \(\mathbf{J}_{\mathbf{f}}\).

Notes

If a diff-Lipschitz constant is known apriori, it can be stored in the instance as follows:

class TestOp(DiffMap):
    def __init__(self, dim_shape, codim_shape):
        super().__init__(dim_shape, codim_shape)
        self.diff_lipschitz = 2

op = TestOp(2, 3)
op.diff_lipschitz  # => 2

Alternatively the diff-Lipschitz constant can be set manually after initialization:

class TestOp(DiffMap):
    def __init__(self, dim_shape, codim_shape):
        super().__init__(dim_shape, codim_shape)

op = TestOp(2, 3)
op.diff_lipschitz  # => inf, since unknown apriori

op.diff_lipschitz = 2  # post-init specification
op.diff_lipschitz  # => 2

diff_lipschitz() never computes anything: call estimate_diff_lipschitz() manually to compute a new diff-Lipschitz estimate:
```
op.diff_lipschitz = op.estimate_diff_lipschitz()
```

estimate_diff_lipschitz(**kwargs)[source]#

Compute a Lipschitz constant of jacobian().

Parameters:: kwargs (Mapping) – Class-specific kwargs to configure diff-Lipschitz estimation.
Return type:: Real

Notes

This method should always be callable without specifying any kwargs.
A Lipschitz constant \(L_{\mathbf{J}_{\mathbf{f}}} > 0\) of the Jacobian map \(\mathbf{J}_{\mathbf{f}}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{(N_{1} \times\cdots\times N_{K}) \times (M_{1} \times\cdots\times M_{D})}\) is such that:

\[\|\mathbf{J}_{\mathbf{f}}(\mathbf{x}) - \mathbf{J}_{\mathbf{f}}(\mathbf{y})\|_{\mathbb{R}^{(N_{1} \times\cdots\times N_{K}) \times (M_{1} \times\cdots\times M_{D})}} \leq L_{\mathbf{J}_{\mathbf{f}}} \|\mathbf{x} - \mathbf{y}\|_{\mathbb{R}^{M_{1} \times\cdots\times M_{D}}}, \qquad \forall \mathbf{x}, \mathbf{y} \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}},\]

where \(\|\cdot\|_{\mathbb{R}^{(N_{1} \times\cdots\times N_{K}) \times (M_{1} \times\cdots\times M_{D})}}\) and \(\|\cdot\|_{\mathbb{R}^{M_{1} \times\cdots\times M_{D}}}\) are the canonical norms on their respective spaces.

The smallest Lipschitz constant of the Jacobian is called the optimal diff-Lipschitz constant.

class DiffFunc(dim_shape, codim_shape)[source]#

Bases: DiffMap, Func

Base class for real-valued differentiable functionals \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}\).

Instances of this class must implement apply() and grad().

If \(f\) and/or its derivative \(f'\) are Lipschitz-continuous with known Lipschitz constants \(L\) and \(\partial L\), the latter should be stored in the lipschitz and diff_lipschitz properties.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

grad(arr)[source]#

Evaluate operator gradient at specified point(s).

Parameters:: arr (NDArray) – (…, M1,…,MD) input points.
Returns:: out – (…, M1,…,MD) gradients.
Return type:: NDArray

Notes

The gradient of a functional \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}\) is given, for every \(\mathbf{x} \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\), by

\[\begin{split}\nabla f(\mathbf{x}) := \left[\begin{array}{c} \frac{\partial f}{\partial x_{1}}(\mathbf{x}) \\ \vdots \\ \frac{\partial f}{\partial x_{M}}(\mathbf{x}) \end{array}\right].\end{split}\]

class ProxFunc(dim_shape, codim_shape)[source]#

Bases: Func

Base class for real-valued proximable functionals \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R} \cup \{+\infty\}\).

A functional \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R} \cup \{+\infty\}\) is said proximable if its proximity operator (see prox() for a definition) admits a simple closed-form expression or can be evaluated efficiently and with high accuracy.

Instances of this class must implement apply() and prox().

If \(f\) is Lipschitz-continuous with known Lipschitz constant \(L\), the latter should be stored in the lipschitz property.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

prox(arr, tau)[source]#

Evaluate proximity operator of \(\tau f\) at specified point(s).

Parameters:

arr (NDArray) – (…, M1,…,MD) input points.
tau (Real) – Positive scale factor.

Returns:

out – (…, M1,…,MD) proximal evaluations.

Return type:

NDArray

Notes

For \(\tau >0\), the proximity operator of a scaled functional \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}\) is defined as:

\[\mathbf{\text{prox}}_{\tau f}(\mathbf{z}) := \arg\min_{\mathbf{x}\in\mathbb{R}^{M_{1} \times\cdots\times M_{D}}} f(x)+\frac{1}{2\tau} \|\mathbf{x}-\mathbf{z}\|_{2}^{2}, \quad \forall \mathbf{z} \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}}.\]

fenchel_prox(arr, sigma)[source]#

Evaluate proximity operator of \(\sigma f^{\ast}\), the scaled Fenchel conjugate of \(f\), at specified point(s).

Parameters:

arr (NDArray) – (…, M1,…,MD) input points.
sigma (Real) – Positive scale factor.

Returns:

out – (…, M1,…,MD) proximal evaluations.

Return type:

NDArray

Notes

For \(\sigma > 0\), the Fenchel conjugate is defined as:

\[f^{\ast}(\mathbf{z}) := \max_{\mathbf{x}\in\mathbb{R}^{M_{1} \times\cdots\times M_{D}}} \langle \mathbf{x},\mathbf{z} \rangle - f(\mathbf{x}).\]

From Moreau’s identity, its proximal operator is given by:

\[\mathbf{\text{prox}}_{\sigma f^{\ast}}(\mathbf{z}) = \mathbf{z} - \sigma \mathbf{\text{prox}}_{f/\sigma}(\mathbf{z}/\sigma).\]

moreau_envelope(mu)[source]#

Approximate proximable functional \(f\) by its Moreau envelope \(f^{\mu}\).

Parameters:: mu (Real) – Positive regularization parameter.
Returns:: op – Differential Moreau envelope.
Return type:: OpT

Notes

Consider a convex non-smooth proximable functional \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R} \cup \{+\infty\}\) and a regularization parameter \(\mu > 0\). The \(\mu\)-Moreau envelope (or Moreau-Yoshida envelope) of \(f\) is given by

\[f^{\mu}(\mathbf{x}) = \min_{\mathbf{z} \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}}} f(\mathbf{z}) \quad + \quad \frac{1}{2\mu} \|\mathbf{x} - \mathbf{z}\|^{2}.\]

The parameter \(\mu\) controls the trade-off between the regularity properties of \(f^{\mu}\) and the approximation error incurred by the Moreau-Yoshida regularization.

The Moreau envelope inherits the convexity of \(f\) and is gradient-Lipschitz (with Lipschitz constant \(\mu^{-1}\)), even if \(f\) is non-smooth. Its gradient is moreover given by:

\[\nabla f^{\mu}(\mathbf{x}) = \mu^{-1} \left(\mathbf{x} - \text{prox}_{\mu f}(\mathbf{x})\right).\]

In addition, \(f^{\mu}\) envelopes \(f\) from below: \(f^{\mu}(\mathbf{x}) \leq f(\mathbf{x})\). This envelope becomes tighter as \(\mu \to 0\):

\[\lim_{\mu \to 0} f^{\mu}(\mathbf{x}) = f(\mathbf{x}).\]

Finally, it can be shown that the minimizers of \(f\) and \(f^{\mu}\) coincide, and that the Fenchel conjugate of \(f^{\mu}\) is strongly-convex.

Example

Construct and plot the Moreau envelope of the \(\ell_{1}\)-norm:

import numpy as np
import matplotlib.pyplot as plt
from pyxu.abc import ProxFunc

class L1Norm(ProxFunc):
    def __init__(self, dim: int):
        super().__init__(dim_shape=dim, codim_shape=1)
    def apply(self, arr):
        return np.linalg.norm(arr, axis=-1, keepdims=True, ord=1)
    def prox(self, arr, tau):
        return np.clip(np.abs(arr)-tau, a_min=0, a_max=None) * np.sign(arr)

mu = [0.1, 0.5, 1]
f = [L1Norm(dim=1).moreau_envelope(_mu) for _mu in mu]
x = np.linspace(-1, 1, 512).reshape(-1, 1)  # evaluation points

fig, ax = plt.subplots(ncols=2)
for _mu, _f in zip(mu, f):
    ax[0].plot(x, _f(x), label=f"mu={_mu}")
    ax[1].plot(x, _f.grad(x), label=f"mu={_mu}")
ax[0].set_title('Moreau Envelope')
ax[1].set_title("Derivative of Moreau Envelope")
for _ax in ax:
    _ax.legend()
    _ax.set_aspect("equal")
fig.tight_layout()

(Source code, png, hires.png, pdf)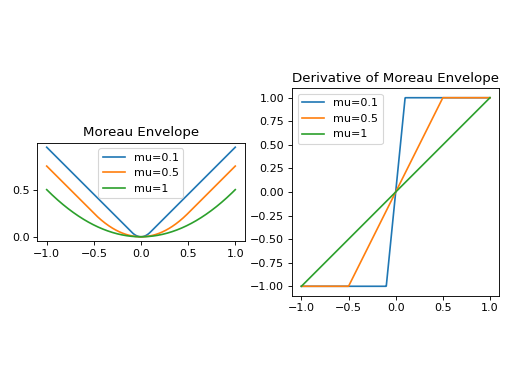

class ProxDiffFunc(dim_shape, codim_shape)[source]#

Bases: ProxFunc, DiffFunc

Base class for real-valued differentiable and proximable functionals \(f:\mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}\).

Instances of this class must implement apply(), grad(), and prox().

If \(f\) and/or its derivative \(f'\) are Lipschitz-continuous with known Lipschitz constants \(L\) and \(\partial L\), the latter should be stored in the lipschitz and diff_lipschitz properties.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

class QuadraticFunc(dim_shape, codim_shape, Q=None, c=None, t=0)[source]#

Bases: ProxDiffFunc

Base class for quadratic functionals \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R} \cup \{+\infty\}\).

The quadratic functional is defined as:

\[f(\mathbf{x}) = \frac{1}{2} \langle\mathbf{x}, \mathbf{Q}\mathbf{x}\rangle + \langle\mathbf{c},\mathbf{x}\rangle + t, \qquad \forall \mathbf{x} \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}},\]

where \(Q\) is a positive-definite operator \(\mathbf{Q}:\mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\), \(\mathbf{c} \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\), and \(t > 0\).

Its gradient is given by:

\[\nabla f(\mathbf{x}) = \mathbf{Q}\mathbf{x} + \mathbf{c}.\]

Its proximity operator by:

\[\text{prox}_{\tau f}(x) = \left( \mathbf{Q} + \tau^{-1} \mathbf{Id} \right)^{-1} \left( \tau^{-1}\mathbf{x} - \mathbf{c} \right).\]

In practice the proximity operator is evaluated via CG.

The Lipschitz constant \(L\) of a quadratic on an unbounded domain is unbounded. The Lipschitz constant \(\partial L\) of \(\nabla f\) is given by the spectral norm of \(\mathbf{Q}\).

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])
Q (PosDefOp)
c (LinFunc)
t (Real)

__init__(dim_shape, codim_shape, Q=None, c=None, t=0)[source]#

Parameters:

Q (PosDefOp) – Positive-definite operator. (Default: Identity)
c (LinFunc) – Linear functional. (Default: NullFunc)
t (Real) – Offset. (Default: 0)
dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

_quad_spec()[source]#

Canonical quadratic parameterization.

Useful for some internal methods, and overloaded during operator arithmetic.

class LinOp(dim_shape, codim_shape)[source]#

Bases: DiffMap

Base class for real-valued linear operators \(\mathbf{A}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\).

Instances of this class must implement apply() and adjoint().

If known, the Lipschitz constant \(L\) should be stored in the lipschitz property.

The Jacobian of a linear map \(\mathbf{A}\) is constant.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

adjoint(arr)[source]#

Evaluate operator adjoint at specified point(s).

Parameters:: arr (NDArray) – (…, N1,…,NK) input points.
Returns:: out – (…, M1,…,MD) adjoint evaluations.
Return type:: NDArray

Notes

The adjoint \(\mathbf{A}^{\ast}: \mathbb{R}^{N_{1} \times\cdots\times N_{K}} \to \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\) of \(\mathbf{A}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\) is defined as:

\[\langle \mathbf{x}, \mathbf{A}^{\ast}\mathbf{y}\rangle_{\mathbb{R}^{M_{1} \times\cdots\times M_{D}}} := \langle \mathbf{A}\mathbf{x}, \mathbf{y}\rangle_{\mathbb{R}^{N_{1} \times\cdots\times N_{K}}}, \qquad \forall (\mathbf{x},\mathbf{y})\in \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \times \mathbb{R}^{N_{1} \times\cdots\times N_{K}}.\]

property T: OpT#: Return the adjoint of \(\mathbf{A}\).

estimate_lipschitz(**kwargs)[source]#

Compute a Lipschitz constant of the operator.

Parameters:

method ("svd" | "trace") –
- If svd, compute the optimal Lipschitz constant.
- If trace, compute an upper bound. (Default)
kwargs –
Optional kwargs passed on to:
- svd: svdvals()
- trace: hutchpp()

Return type:

Real

Notes

The tightest Lipschitz constant is given by the spectral norm of the operator \(\mathbf{A}\): \(\|\mathbf{A}\|_{2}\). It can be computed via the SVD, which is compute-intensive task for large operators. In this setting, it may be advantageous to overestimate the Lipschitz constant with the Frobenius norm of \(\mathbf{A}\) since \(\|\mathbf{A}\|_{F} \geq \|\mathbf{A}\|_{2}\).

\(\|\mathbf{A}\|_{F}\) can be efficiently approximated by computing the trace of \(\mathbf{A}^{\ast} \mathbf{A}\) (or \(\mathbf{A}\mathbf{A}^{\ast}\)) via the Hutch++ stochastic algorithm.
\(\|\mathbf{A}\|_{F}\) is upper-bounded by \(\|\mathbf{A}\|_{F} \leq \sqrt{n} \|\mathbf{A}\|_{2}\), where the equality is reached (worst-case scenario) when the eigenspectrum of the linear operator is flat.

svdvals(k, gpu=False, dtype=None, **kwargs)[source]#

Compute leading singular values of the linear operator.

Parameters:

k (Integer) – Number of singular values to compute.
gpu (bool) – If True the singular value decomposition is performed on the GPU.
dtype (DType) – Working precision of the linear operator.
kwargs (Mapping) – Additional kwargs accepted by svds().

Returns:

D – (k,) singular values in ascending order.

Return type:

NDArray

asarray(xp=None, dtype=None)[source]#

Matrix representation of the linear operator.

Parameters:

xp (ArrayModule) – Which array module to use to represent the output. (Default: NumPy.)
dtype (DType) – Precision of the array. (Default: current runtime precision.)

Returns:

A – (*codim_shape, *dim_shape) array-representation of the operator.

Return type:

NDArray

Note

This generic implementation assumes the operator is backend-agnostic. Thus, when defining a new backend-specific operator, asarray() may need to be overriden.

gram()[source]#

Gram operator \(\mathbf{A}^{\ast} \mathbf{A}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\).

Returns:: op – Gram operator.
Return type:: OpT

Note

By default the Gram is computed by the composition self.T * self. This may not be the fastest way to compute the Gram operator. If the Gram can be computed more efficiently (e.g. with a convolution), the user should re-define this method.

cogram()[source]#

Co-Gram operator \(\mathbf{A}\mathbf{A}^{\ast}:\mathbb{R}^{N_{1} \times\cdots\times N_{K}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\).

Returns:: op – Co-Gram operator.
Return type:: OpT

Note

By default the co-Gram is computed by the composition self * self.T. This may not be the fastest way to compute the co-Gram operator. If the co-Gram can be computed more efficiently (e.g. with a convolution), the user should re-define this method.

pinv(arr, damp, kwargs_init=None, kwargs_fit=None)[source]#

Evaluate the Moore-Penrose pseudo-inverse \(\mathbf{A}^{\dagger}\) at specified point(s).

Parameters:

arr (NDArray) – (…, N1,…,NK) input points.
damp (Real) – Positive dampening factor regularizing the pseudo-inverse.
kwargs_init (Mapping) – Optional kwargs to be passed to CG()’s __init__() method.
kwargs_fit (Mapping) – Optional kwargs to be passed to CG()’s fit() method.

Returns:

out – (…, M1,…,MD) pseudo-inverse(s).

Return type:

NDArray

Notes

The Moore-Penrose pseudo-inverse of an operator \(\mathbf{A}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\) is defined as the operator \(\mathbf{A}^{\dagger}: \mathbb{R}^{N_{1} \times\cdots\times N_{K}} \to \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\) verifying the Moore-Penrose conditions:

\(\mathbf{A} \mathbf{A}^{\dagger} \mathbf{A} = \mathbf{A}\),

\(\mathbf{A}^{\dagger} \mathbf{A} \mathbf{A}^{\dagger} = \mathbf{A}^{\dagger}\),

\((\mathbf{A}^{\dagger} \mathbf{A})^{\ast} = \mathbf{A}^{\dagger} \mathbf{A}\),

\((\mathbf{A} \mathbf{A}^{\dagger})^{\ast} = \mathbf{A} \mathbf{A}^{\dagger}\).

This operator exists and is unique for any finite-dimensional linear operator. The action of the pseudo-inverse \(\mathbf{A}^{\dagger} \mathbf{y}\) for every \(\mathbf{y} \in \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\) can be computed in matrix-free fashion by solving the normal equations:

\[\mathbf{A}^{\ast} \mathbf{A} \mathbf{x} = \mathbf{A}^{\ast} \mathbf{y} \quad\Leftrightarrow\quad \mathbf{x} = \mathbf{A}^{\dagger} \mathbf{y}, \quad \forall (\mathbf{x}, \mathbf{y}) \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \times \mathbb{R}^{N_{1} \times\cdots\times N_{K}}.\]

In the case of severe ill-conditioning, it is possible to consider the dampened normal equations for a numerically-stabler approximation of \(\mathbf{A}^{\dagger} \mathbf{y}\):

\[(\mathbf{A}^{\ast} \mathbf{A} + \tau I) \mathbf{x} = \mathbf{A}^{\ast} \mathbf{y},\]

where \(\tau > 0\) corresponds to the damp parameter.

dagger(damp, kwargs_init=None, kwargs_fit=None)[source]#

Return the Moore-Penrose pseudo-inverse operator \(\mathbf{A}^\dagger\).

Parameters:

damp (Real) – Positive dampening factor regularizing the pseudo-inverse.
kwargs_init (Mapping) – Optional kwargs to be passed to CG()’s __init__() method.
kwargs_fit (Mapping) – Optional kwargs to be passed to CG()’s fit() method.

Returns:

op – Moore-Penrose pseudo-inverse operator.

Return type:

OpT

classmethod from_array(A, dim_rank=None, enable_warnings=True)[source]#

Instantiate a LinOp from its array representation.

Parameters:

A (NDArray) – (*codim_shape, *dim_shape) array.
dim_rank (Integer) – Dimension rank \(D\). (Can be omitted if A is 2D.)
enable_warnings (bool) – If True, emit a warning in case of precision mis-match issues.

Returns:

op – Linear operator

Return type:

OpT

class SquareOp(dim_shape, codim_shape)[source]#

Bases: LinOp

Base class for square linear operators, i.e. \(\mathbf{A}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\) (endomorphsisms).

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

trace(**kwargs)[source]#

Compute trace of the operator.

Parameters:

method ("explicit" | "hutchpp") –
- If explicit, compute the exact trace.
- If hutchpp, compute an approximation. (Default)
kwargs (Mapping) –
Optional kwargs passed to:
- explicit: trace()
- hutchpp: hutchpp()

Returns:

tr – Trace estimate.

Return type:

Real

class NormalOp(dim_shape, codim_shape)[source]#

Bases: SquareOp

Base class for normal operators.

Normal operators satisfy the relation \(\mathbf{A} \mathbf{A}^{\ast} = \mathbf{A}^{\ast} \mathbf{A}\). It can be shown that an operator is normal iff it is unitarily diagonalizable, i.e. \(\mathbf{A} = \mathbf{U} \mathbf{D} \mathbf{U}^{\ast}\).

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

class SelfAdjointOp(dim_shape, codim_shape)[source]#

Bases: NormalOp

Base class for self-adjoint operators.

Self-adjoint operators satisfy the relation \(\mathbf{A}^{\ast} = \mathbf{A}\).

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

class UnitOp(dim_shape, codim_shape)[source]#

Bases: NormalOp

Base class for unitary operators.

Unitary operators satisfy the relation \(\mathbf{A} \mathbf{A}^{\ast} = \mathbf{A}^{\ast} \mathbf{A} = I\).

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

class ProjOp(dim_shape, codim_shape)[source]#

Bases: SquareOp

Base class for projection operators.

Projection operators are idempotent, i.e. \(\mathbf{A}^{2} = \mathbf{A}\).

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

class OrthProjOp(dim_shape, codim_shape)[source]#

Bases: ProjOp, SelfAdjointOp

Base class for orthogonal projection operators.

Orthogonal projection operators are idempotent and self-adjoint, i.e. \(\mathbf{A}^{2} = \mathbf{A}\) and \(\mathbf{A}^{\ast} = \mathbf{A}\).

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

class PosDefOp(dim_shape, codim_shape)[source]#

Bases: SelfAdjointOp

Base class for positive-definite operators.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

class LinFunc(dim_shape, codim_shape)[source]#

Bases: ProxDiffFunc, LinOp

Base class for real-valued linear functionals \(f: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}\).

Instances of this class must implement apply(), and adjoint().

If known, the Lipschitz constant \(L\) should be stored in the lipschitz property.

Parameters:

dim_shape (Integral | tuple[Integral, ...])
codim_shape (Integral | tuple[Integral, ...])

pyxu.abc.solver #

class Solver(*, folder=None, exist_ok=False, stop_rate=1, writeback_rate=None, verbosity=None, show_progress=True, log_var=frozenset({}))[source]#

Bases: object

Iterative solver for minimization problems of the form \(\hat{x} = \arg\min_{x \in \mathbb{R}^{M_{1} \times\cdots\times M_{D}}} \mathcal{F}(x)\), where the form of \(\mathcal{F}\) is solver-dependent.

Solver provides a versatile API for solving optimisation problems, with the following features:

manual/automatic/background execution of solver iterations via parameters provided to fit(). (See below.)
automatic checkpointing of solver progress, providing a safe restore point in case of faulty numerical code. Each solver instance backs its state and final output to a folder on disk for post-analysis. In particular fit() should never crash: detailed exception information will always be available in a logfile for post-analysis.
arbitrary specification of complex stopping criteria via the StoppingCriterion class.
solve for multiple initial points in parallel. (Not always supported by all solvers.)

To implement a new iterative solver, users need to sub-class Solver and overwrite the methods below:

__init__()
m_init() [i.e. math-init()]
m_step() [i.e. math-step()]
default_stop_crit() [optional; see method definition for details]
objective_func() [optional; see method definition for details]

Advanced functionalities of Solver are automatically inherited by sub-classes.

Examples

Here are examples on how to solve minimization problems with this class:

slvr = Solver()

### 1. Blocking mode: .fit() does not return until solver has stopped.
>>> slvr.fit(mode=SolverMode.BLOCK, ...)
>>> data, hist = slvr.stats()  # final output of solver.

### 2. Async mode: solver iterations run in the background.
>>> slvr.fit(mode=SolverMode.ASYNC, ...)
>>> print('test')  # you can do something in between.
>>> slvr.busy()  # or check whether the solver already stopped.
>>> slvr.stop()  # and preemptively force it to stop.
>>> data, hist = slvr.stats()  # then query the result after a (potential) force-stop.

### 3. Manual mode: fine-grain control of solver data per iteration.
>>> slvr.fit(mode=SolverMode.MANUAL, ...)
>>> for data in slvr.steps():
...     # Do something with the logged variables after each iteration.
...     pass  # solver has stopped after the loop.
>>> data, hist = slvr.stats()  # final output of solver.

Parameters:

folder (str | Path)
exist_ok (bool)
stop_rate (Integral)
writeback_rate (Integral)
verbosity (Integral)
show_progress (bool)
log_var (str | Collection[str])

_mstate: dict[str, Any]#: Mathematical state.

_astate: dict[str, Any]#: Book-keeping (non-math) state.

__init__(*, folder=None, exist_ok=False, stop_rate=1, writeback_rate=None, verbosity=None, show_progress=True, log_var=frozenset({}))[source]#

Parameters:

folder (Path) – Directory on disk where instance data should be stored. A location will be automatically chosen if unspecified. (Default: OS-dependent tempdir.)
exist_ok (bool) – If folder is specified and exist_ok is false (default), FileExistsError is raised if the target directory already exists.
stop_rate (Integer) – Rate at which solver evaluates stopping criteria.
writeback_rate (Integer) –
Rate at which solver checkpoints are written to disk:
- If None (default), all checkpoints are disabled: the final solver output is only stored in memory.
- If 0, intermediate checkpoints are disabled: only the final solver output will be written to disk.
- Any other integer: checkpoint to disk at provided interval. Must be a multiple of stop_rate.
verbosity (Integer) – Rate at which stopping criteria statistics are logged. Must be a multiple of stop_rate. Defaults to stop_rate if unspecified.
show_progress (bool) – If True (default) and fit() is run with mode=BLOCK, then statistics are also logged to stdout.
log_var (VarName) – Variables from the solver’s math-state (_mstate) to be logged per iteration. These are the variables made available when calling stats().

Notes

Partial device<>CPU synchronization takes place when stopping-criteria are evaluated. Increasing stop_rate is advised to reduce the effect of such transfers when applicable.
Full device<>CPU synchronization takes place at checkpoint-time. Increasing writeback_rate is advised to reduce the effect of such transfers when applicable.

fit(**kwargs)[source]#

Solve minimization problem(s) defined in __init__(), with the provided run-specifc parameters.

Parameters:

kwargs – See class-level docstring for class-specific keyword parameters.
stop_crit (StoppingCriterion) – Stopping criterion to end solver iterations. If unspecified, defaults to default_stop_crit().
mode (SolverMode) –
Execution mode. See Solver for usage examples.

Useful method pairs depending on the execution mode:
- BLOCK: fit()
- ASYNC: fit(), busy(), stop()
- MANUAL: fit(), steps()
track_objective (bool) – Auto-compute objective function every time stopping criterion is evaluated.

m_init(**kwargs)[source]#

Set solver’s initial mathematical state based on kwargs provided to fit().

This method must only manipulate _mstate.

After calling this method, the solver must be able to complete its 1st iteration via a call to m_step().

m_step()[source]#

Perform one (mathematical) step.

This method must only manipulate _mstate.

steps(n=None)[source]#

Generator of logged variables after each iteration.

The i-th call to next() on this object returns the logged variables after the i-th solver iteration.

This method is only usable after calling fit() with mode=MANUAL. See Solver for usage examples.

There is no guarantee that a checkpoint on disk exists when the generator is exhausted. (Reason: potential exceptions raised during solver’s progress.) Users should invoke writeback() afterwards if needed.

Parameters:

n (Integer) –

Maximum number of next() calls allowed before exhausting the generator. Defaults to infinity if unspecified.

The generator will terminate prematurely if the solver naturally stops before n calls to next() are made.

Return type:

Generator

stats()[source]#

Query solver state.

Returns:

data (Mapping) – Value(s) of log_var (s) after last iteration.
history (numpy.ndarray, None) – (N_iter,) records of stopping-criteria values sampled every stop_rate iteration.

Return type:

tuple[dict[str, Real | NDArray | None], ndarray | None]

Notes

If any of the log_var (s) and/or history are not (yet) known at query time, None is returned.

property workdir: str | Path#

Returns:: wd – Absolute path to the directory on disk where instance data is stored.
Return type:: Path

property logfile: str | Path#

Returns:: lf – Absolute path to the log file on disk where stopping criteria statistics are logged.
Return type:: Path

property datafile: str | Path#

Returns:: df – Absolute path to the file on disk where log_var (s) are stored during checkpointing or after solver has stopped.
Return type:: Path

busy()[source]#

Test if an async-running solver has stopped.

This method is only usable after calling fit() with mode=ASYNC. See Solver for usage examples.

Returns:: b – True if solver has stopped, False otherwise.
Return type:: bool

solution()[source]#

Output the “solution” of the optimization problem.

This is a helper method intended for novice users. The return type is sub-class dependent, so don’t write an API using this: use stats() instead.

stop()[source]#

Stop an async-running solver.

This method is only usable after calling fit() with mode=ASYNC. See Solver for usage examples.

This method will block until the solver has stopped.

There is no guarantee that a checkpoint on disk exists once halted. (Reason: potential exceptions raised during solver’s progress.) Users should invoke writeback() afterwards if needed.

Users must call this method to terminate an async-solver, even if busy() is False.

writeback()[source]#: Checkpoint state to disk.

default_stop_crit()[source]#

Default stopping criterion for solver if unspecified in fit() calls.

Sub-classes are expected to overwrite this method. If not overridden, then omitting the stop_crit parameter in fit() is forbidden.

Return type:: StoppingCriterion

objective_func()[source]#

Evaluate objective function given current math state.

The output array must have shape:

(1,) if evaluated at 1 point,
(N, 1) if evaluated at N different points.

Sub-classes are expected to overwrite this method. If not overridden, then enabling track_objective in fit() is forbidden.

Return type:: NDArray

class SolverMode(value, names=<not given>, *values, module=None, qualname=None, type=None, start=1, boundary=None)[source]#

Bases: Enum

Solver execution mode.

BLOCK = 1#

MANUAL = 2#

ASYNC = 3#

class StoppingCriterion[source]#

Bases: object

State machines (SM) which decide when to stop iterative solvers by examining their mathematical state.

SM decisions are always accompanied by at least one numerical statistic. These stats may be queried by solvers via info() to provide diagnostic information to users.

Composite stopping criteria can be implemented via the overloaded (and[&], or[|]) operators.

stop(state)[source]#

Compute a stop signal based on the current mathematical state.

Parameters:

state (Mapping) –

Full mathematical state of solver at some iteration, i.e. _mstate.

Values from state may be cached inside the instance to form complex stopping conditions.

Returns:

s – True if no further iterations should be performed, False otherwise.

Return type:

bool

info()[source]#

Get statistics associated with the last call to stop().

Returns:: data
Return type:: Mapping

clear()[source]#

Clear SM state (if any).

This method is useful when a StoppingCriterion instance must be reused in another call to fit().

pyxu.abc#

pyxu.abc.arithmetic#

pyxu.abc.operator#

pyxu.abc.solver#

pyxu.abc.arithmetic #

pyxu.abc.operator #

pyxu.abc.solver #