pyxu.opt.solver#
- class PGD(f=None, g=None, **kwargs)[source]#
Bases:
SolverProximal Gradient Descent (PGD) solver.
PGD solves minimization problems of the form
\[{\min_{\mathbf{x}\in\mathbb{R}^{M_{1} \times\cdots\times M_{D}}} \; \mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{G}(\mathbf{x})},\]where:
\(\mathcal{F}:\mathbb{R}^{M_{1} \times\cdots\times M_{D}}\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).
\(\mathcal{G}:\mathbb{R}^{M_{1} \times\cdots\times M_{D}}\rightarrow \mathbb{R}\cup\{+\infty\}\) is a proper, lower semicontinuous and convex function with a simple proximal operator.
Remarks#
The problem is feasible – i.e. there exists at least one solution.
The algorithm is still valid if either \(\mathcal{F}\) or \(\mathcal{G}\) is zero.
The convergence is guaranteed for step sizes \(\tau\leq 1/\beta\).
Various acceleration schemes are described in [APGD]. PGD achieves the following (optimal) convergence rate with the implemented acceleration scheme from Chambolle & Dossal:
\[\lim\limits_{n\rightarrow \infty} n^2\left\vert \mathcal{J}(\mathbf{x}^\star)- \mathcal{J}(\mathbf{x}_n)\right\vert=0 \qquad\&\qquad \lim\limits_{n\rightarrow \infty} n^2\Vert \mathbf{x}_n-\mathbf{x}_{n-1}\Vert^2_\mathcal{X}=0,\]for some minimiser \({\mathbf{x}^\star}\in\arg\min_{\mathbf{x}\in\mathbb{R}^{M_{1} \times\cdots\times M_{D}}} \;\left\{\mathcal{J}(\mathbf{x}):=\mathcal{F}(\mathbf{x})+\mathcal{G}(\mathbf{x})\right\}\). In other words, both the objective functional and the PGD iterates \(\{\mathbf{x}_n\}_{n\in\mathbb{N}}\) converge at a rate \(o(1/n^2)\). Significant practical speedup can be achieved for values of \(d\) in the range \([50,100]\) [APGD].
The relative norm change of the primal variable is used as the default stopping criterion. By default, the algorithm stops when the norm of the difference between two consecutive PGD iterates \(\{\mathbf{x}_n\}_{n\in\mathbb{N}}\) is smaller than 1e-4. Different stopping criteria can be used.
Parameters (
__init__())#Parameters (
fit())#x0 (
NDArray) – (…, M1,…,MD) initial point(s).tau (
Real,None) – Gradient step size. Defaults to \(1 / \beta\) if unspecified.acceleration (
bool) – If True (default), then use Chambolle & Dossal acceleration scheme.d (
Real) – Chambolle & Dossal acceleration parameter \(d\). Should be greater than 2. Only meaningful ifaccelerationis True. Defaults to 75 in unspecified.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
- class CG(A, **kwargs)[source]#
Bases:
SolverConjugate Gradient Method.
The Conjugate Gradient method solves the minimization problem
\[\min_{\mathbf{x}\in\mathbb{R}^{M_{1} \times\cdots\times M_{D}}} \frac{1}{2} \langle \mathbf{x}, \mathbf{A} \mathbf{x} \rangle - \langle \mathbf{x}, \mathbf{b} \rangle,\]where \(\mathbf{A}: \mathbb{R}^{{M_{1} \times\cdots\times M_{D}}} \to \mathbb{R}^{{M_{1} \times\cdots\times M_{D}}}\) is a symmetric positive definite operator, and \(\mathbf{b} \in \mathbb{R}^{{M_{1} \times\cdots\times M_{D}}}\).
The norm of the explicit residual \(\mathbf {r}_{k+1}:=\mathbf{b}-\mathbf{Ax}_{k+1}\) is used as the default stopping criterion. This provides a guaranteed level of accuracy both in exact arithmetic and in the presence of round-off errors. By default, the iterations stop when the norm of the explicit residual is smaller than 1e-4.
Parameters (
__init__())#A (
PosDefOp) – Positive-definite operator \(\mathbf{A}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{M_{1} \times\cdots\times M_{D}}\).**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.__init__().
Parameters (
fit())#b (
NDArray) – (…, M1,…,MD) \(\mathbf{b}\) terms in the CG cost function.All problems are solved in parallel.
x0 (
NDArray,None) – (…, M1,…,MD) initial point(s).Must be broadcastable with
bif provided. Defaults to 0.restart_rate (
Integer) – Number of iterations after which restart is applied.By default, a restart is done after ‘n’ iterations, where ‘n’ corresponds to the dimension of \(\mathbf{A}\).
**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
- Parameters:
A (PosDefOp)
- class NLCG(f, **kwargs)[source]#
Bases:
SolverNonlinear Conjugate Gradient Method (NLCG).
The Nonlinear Conjugate Gradient method finds a local minimum of the problem
\[\min_{\mathbf{x}\in\mathbb{R}^{N}} f(\mathbf{x}),\]where \(f: \mathbb{R}^{N} \to \mathbb{R}\) is a differentiable functional. When \(f\) is quadratic, NLCG is equivalent to the Conjugate Gradient (CG) method. NLCG hence has similar convergence behaviour to CG if \(f\) is locally-quadratic. The converge speed may be slower however due to its line-search overhead [NumOpt_NocWri].
The norm of the gradient \(\nabla f_k = \nabla f(\mathbf{x}_k)\) is used as the default stopping criterion. By default, the iterations stop when the norm of the gradient is smaller than 1e-4.
Multiple variants of NLCG exist. They differ mainly in how the weights applied to conjugate directions are updated. Two popular variants are implemented:
The Fletcher-Reeves variant:
\[\beta_k^\text{FR} = \frac{ \Vert{\nabla f_{k+1}}\Vert_{2}^{2} }{ \Vert{\nabla f_{k}}\Vert_{2}^{2} }.\]The Polak-Ribière+ method:
\[\begin{split}\beta_k^\text{PR} = \frac{ \nabla f_{k+1}^T\left(\nabla f_{k+1} - \nabla f_k\right) }{ \Vert{\nabla f_{k}}\Vert_{2}^{2} } \\ \beta_k^\text{PR+} = \max\left(0, \beta_k^\text{PR}\right).\end{split}\]
Parameters (
__init__())#f (
DiffFunc) – Differentiable function \(\mathcal{F}\).**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.__init__().
Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s).variant (“PR”, “FR”) – Name of the NLCG variant to use:
“PR”: Polak-Ribière+ variant (default).
“FR”: Fletcher-Reeves variant.
restart_rate (
Integer,None) – Number of iterations after which restart is applied.By default, restart is done after \(N\) iterations.
**kwargs (
Mapping) – Optional parameters forwarded tobacktracking_linesearch().If
a0is unspecified and \(\nabla f\) is \(\beta\)-Lipschitz continuous, thena0is auto-chosen as \(\beta^{-1}\). Users are expected to seta0if its value cannot be auto-inferred.Other keyword parameters are passed on to
pyxu.abc.Solver.fit().
Example
Consider the following quadratic optimization problem:
This problem is strictly convex, hence NLCG will converge to the optimal solution:
import numpy as np import pyxu.operator as pxo import pyxu.opt.solver as pxsl N, a, b = 5, 3, 1 f = pxo.SquaredL2Norm(N).asloss(b).argscale(a) # \norm(Ax - b)**2 nlcg = pxsl.NLCG(f) nlcg.fit(x0=np.zeros((N,)), variant="FR") x_opt = nlcg.solution() np.allclose(x_opt, 1/a) # True
Note however that the CG method is preferable in this context since it omits the linesearch overhead. The former depends on the cost of applying \(A\), and may be significant.
- Parameters:
f (DiffFunc)
- class Adam(f, **kwargs)[source]#
Bases:
SolverAdam solver [ProxAdam].
Adam minimizes
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\mathcal{F}(\mathbf{x})},\]where:
\(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).
Adam is a suitable alternative to Proximal Gradient Descent (
PGD) when:the cost function is differentiable,
computing \(\beta\) to optimally choose the step size is infeasible,
line-search methods to estimate step sizes are too expensive.
Compared to PGD, Adam auto-tunes gradient updates based on stochastic estimates of \(\phi_{t} = \mathbb{E}[\nabla\mathcal{F}]\) and \(\psi_{t} = \mathbb{E}[\nabla\mathcal{F}^{2}]\) respectively.
Adam has many named variants for particular choices of \(\phi\) and \(\psi\):
Adam:
\[\phi_t = \frac{ \mathbf{m}_t }{ 1-\beta_1^t } \qquad \psi_t = \sqrt{ \frac{ \mathbf{v}_t }{ 1-\beta_2^t } } + \epsilon,\]AMSGrad:
\[\phi_t = \mathbf{m}_t \qquad \psi_t = \sqrt{\hat{\mathbf{v}}_t},\]PAdam:
\[\phi_t = \mathbf{m}_t \qquad \psi_t = \hat{\mathbf{v}}_t^p,\]
where in all cases:
\[\begin{split}\mathbf{m}_t = \beta_1\mathbf{m}_{t-1} + (1-\beta_1)\mathbf{g}_t \\ \mathbf{v}_t = \beta_2\mathbf{v}_{t-1} + (1-\beta_2)\mathbf{g}_t^2\\ \hat{\mathbf{v}}_t = \max(\hat{\mathbf{v}}_{t-1}, \mathbf{v}_t),\end{split}\]with \(\mathbf{m}_0 = \mathbf{v}_0 = \mathbf{0}\).
Remarks#
The convergence is guaranteed for step sizes \(\alpha\leq 2/\beta\).
The default stopping criterion is the relative norm change of the primal variable. By default, the algorithm stops when the norm of the difference between two consecutive iterates \(\{\mathbf{x}_n\}_{n\in\mathbb{N}}\) is smaller than 1e-4. Different stopping criteria can be used. It is recommended to change the stopping criterion when using the PAdam and AMSGrad variants to avoid premature stops.
Parameters (
__init__())#f (
DiffFunc) – Differentiable function \(\mathcal{F}\).**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.__init__().
Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s).variant (“adam”, “amsgrad”, “padam”) – Name of the Adam variant to use. Defaults to “adam”.
a (
Real,None) – Max normalized gradient step size. Defaults to \(1 / \beta\) if unspecified.b1 (
Real) – 1st-order gradient exponential decay \(\beta_{1} \in [0, 1)\).b2 (
Real) – 2nd-order gradient exponential decay \(\beta_{2} \in [0, 1)\).m0 (
NDArray,None) – (…, N) initial 1st-order gradient estimate corresponding to each initial point. Defaults to the null vector if unspecified.v0 (
NDArray,None) – (…, N) initial 2nd-order gradient estimate corresponding to each initial point. Defaults to the null vector if unspecified.p (
Real) – PAdam power parameter \(p \in (0, 0.5]\). Must be specified for PAdam, unused otherwise.eps_adam (
Real) – Adam noise parameter \(\epsilon\). This term is used exclusively ifvariant="adam". Defaults to 1e-6.eps_var (
Real) – Avoids division by zero if estimated gradient variance is too small. Defaults to 1e-6.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
Note
If provided,
m0andv0must be broadcastable withx0.Example
Consider the following optimization problem:
\[\min_{\mathbf{x}\in\mathbb{R}^N} \Vert{\mathbf{x}-\mathbf{1}}\Vert_2^2\]import numpy as np from pyxu.operator import SquaredL2Norm from pyxu.opt.solver import Adam N = 3 f = SquaredL2Norm(dim=N).asloss(1) slvr = Adam(f) slvr.fit( x0=np.zeros((N,)), variant="padam", p=0.25, ) x_opt = slvr.solution() np.allclose(x_opt, 1, rtol=1e-4) # True
- Parameters:
f (DiffFunc)
- class CondatVu(f=None, g=None, h=None, K=None, **kwargs)[source]#
Bases:
_PrimalDualSplittingCondat-Vu primal-dual splitting algorithm.
This solver is also accessible via the alias
CV.The Condat-Vu (CV) primal-dual method is described in [CVS]. (This particular implementation is based on the pseudo-code Algorithm 7.1 provided in [FuncSphere] Chapter 7, Section1.)
It can be used to solve problems of the form:
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{G}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathcal{K} \mathbf{x})},\]where:
\(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).
\(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) and \(\mathcal{H}:\mathbb{R}^M\rightarrow \mathbb{R}\cup\{+\infty\}\) are proper, lower semicontinuous and convex functions with simple proximal operators.
\(\mathcal{K}:\mathbb{R}^N\rightarrow \mathbb{R}^M\) is a differentiable map (e.g. a linear operator \(\mathbf{K}\)), with operator norm:
\[\Vert{\mathcal{K}}\Vert_2=\sup_{\mathbf{x}\in\mathbb{R}^N,\Vert\mathbf{x}\Vert_2=1} \Vert\mathcal{K}(\mathbf{x})\Vert_2.\]
Remarks#
The problem is feasible, i.e. there exists at least one solution.
The algorithm is still valid if one or more of the terms \(\mathcal{F}\), \(\mathcal{G}\) or \(\mathcal{H}\) is zero.
The algorithm has convergence guarantees when \(\mathcal{H}\) is composed with a linear operator \(\mathbf{K}\). When \(\mathcal{F}=0\), convergence can be proven for non-linear differentiable maps \(\mathcal{K}\) (see [NLCP]). Note that
CondatVudoes not yet support automatic selection of hyperparameters for the case of non-linear differentiable maps \(\mathcal{K}\).Assume that either of the following holds:
\(\beta>0\) and:
\(\gamma \geq \frac{\beta}{2}\),
\(\frac{1}{\tau}-\sigma\Vert\mathbf{K}\Vert_{2}^2\geq \gamma\),
\(\rho \in ]0,\delta[\), where \(\delta:=2-\frac{\beta}{2}\gamma^{-1}\in[1,2[\) (\(\delta=2\) is possible when \(\mathcal{F}\) is quadratic and \(\gamma \geq \beta\), see [PSA]).
\(\beta=0\) and:
\(\tau\sigma\Vert\mathbf{K}\Vert_{2}^2\leq 1\),
\(\rho \in ]0,2[\).
Then there exists a pair \((\mathbf{x}^\star,\mathbf{z}^\star)\in\mathbb{R}^N\times \mathbb{R}^M\) solution s.t. the primal and dual sequences of estimates \((\mathbf{x}_n)_{n\in\mathbb{N}}\) and \((\mathbf{z}_n)_{n\in\mathbb{N}}\) converge towards \(\mathbf{x}^\star\) and \(\mathbf{z}^\star\) respectively, i.e.
\[\lim_{n\rightarrow +\infty}\Vert\mathbf{x}^\star-\mathbf{x}_n\Vert_2=0, \quad \text{and} \quad \lim_{n\rightarrow +\infty}\Vert\mathbf{z}^\star-\mathbf{z}_n\Vert_2=0.\]
Parameters (
__init__())#Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.z0 (
NDArray,None) – (…, M) initial point(s) for the dual variable. IfNone(default), then useK(x0)as the initial point for the dual variable.beta (
Real,None) – Lipschitz constant \(\beta\) of \(\nabla\mathcal{F}\). If not provided, it will be automatically estimated.tuning_strategy (1, 2, 3) – Strategy to be employed when setting the hyperparameters (default to 1). See section below for more details.
**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
Default hyperparameter values
This class supports three strategies to automatically set the hyperparameters (see [PSA] for more details and numerical experiments comparing the performance of the three strategies):
tuning_strategy == 1: \(\gamma = \beta\) (safe step sizes) and \(\rho=1\) (no relaxation).This is the most standard way of setting the parameters in the literature.
tuning_strategy == 2: \(\gamma = \beta/1.9\) (large step sizes) and \(\rho=1\) (no relaxation).This strategy favours large step sizes forbidding the use of overrelaxation. When \(\beta=0\), coincides with the first strategy.
tuning_strategy == 3: \(\gamma = \beta\) (safe step sizes) and \(\rho=\delta - 0.1 > 1\) (overrelaxation).This strategy chooses smaller step sizes, but performs overrelaxation.
Once \(\gamma\) chosen, the convergence speed of the algorithm is improved by choosing \(\sigma\) and \(\tau\) as large as possible and relatively well-balanced – so that both the primal and dual variables converge at the same pace. Whenever possible, we therefore choose perfectly balanced parameters \(\sigma=\tau\) saturating the convergence inequalities for a given value of \(\gamma\).
For \(\beta>0\) and \(\mathcal{H}\neq 0\) this yields:
\[\frac{1}{\tau}-\tau\Vert\mathbf{K}\Vert_{2}^2= \gamma \quad\Longleftrightarrow\quad -\tau^2\Vert\mathbf{K}\Vert_{2}^2-\gamma\tau+1=0,\]which admits one positive root
\[\tau=\sigma=\frac{1}{\Vert\mathbf{K}\Vert_{2}^2}\left(-\frac{\gamma}{2}+\sqrt{\frac{\gamma^2}{4}+\Vert\mathbf{K}\Vert_{2}^2}\right).\]For \(\beta>0\) and \(\mathcal{H}=0\) this yields: \(\tau=1/\gamma.\)
For \(\beta=0\) this yields: \(\tau=\sigma=\Vert\mathbf{K}\Vert_{2}^{-1}\).
When \(\tau\) is provided (\(\tau = \tau_{1}\)), but not \(\sigma\), the latter is chosen as:
\[\frac{1}{\tau_{1}}-\sigma\Vert\mathbf{K}\Vert_{2}^2= \gamma \quad\Longleftrightarrow\quad \sigma=\left(\frac{1}{\tau_{1}}-\gamma\right)\frac{1}{\Vert\mathbf{K}\Vert_{2}^2}.\]When \(\sigma\) is provided (\(\sigma = \sigma_{1}\)), but not \(\tau\), the latter is chosen as:
\[\frac{1}{\tau}-\sigma_{1}\Vert\mathbf{K}\Vert_{2}^2= \gamma \quad\Longleftrightarrow\quad \tau=\frac{1}{\left(\gamma+\sigma_{1}\Vert\mathbf{K}\Vert_{2}^2\right)}.\]Warning
When values are provided for both \(\tau\) and \(\sigma\), it is assumed that the latter satisfy the convergence inequalities, but no check is explicitly performed. Automatic selection of hyperparameters for the case of non-linear differentiable maps \(\mathcal{K}\) is not supported yet.
Example
Consider the following optimisation problem:
\[\min_{\mathbf{x}\in\mathbb{R}_+^N}\frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\quad+\quad\lambda_1 \|\mathbf{D}\mathbf{x}\|_1\quad+\quad\lambda_2 \|\mathbf{x}\|_1,\]with \(\mathbf{D}\in\mathbb{R}^{N\times N}\) the discrete derivative operator and \(\mathbf{G}\in\mathbb{R}^{L\times N}, \, \mathbf{y}\in\mathbb{R}^L, \lambda_1,\lambda_2>0.\) This problem can be solved via PDS with \(\mathcal{F}(\mathbf{x})= \frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\), \(\mathcal{G}(\mathbf{x})=\lambda_2\|\mathbf{x}\|_1,\) \(\mathcal{H}(\mathbf{x})=\lambda \|\mathbf{x}\|_1\) and \(\mathbf{K}=\mathbf{D}\).
import matplotlib.pyplot as plt import numpy as np import pyxu.operator as pxo from pyxu.operator import SubSample, PartialDerivative from pyxu.opt.solver import CV x = np.repeat(np.asarray([0, 2, 1, 3, 0, 2, 0]), 10) N = x.size D = PartialDerivative.finite_difference(dim_shape=(N,), order=(1,)) downsample = SubSample(N, slice(None, None, 3)) y = downsample(x) loss = (1 / 2) * pxo.SquaredL2Norm(y.size).argshift(-y) F = loss * downsample cv = CV(f=F, g=0.01 * pxo.L1Norm(N), h=0.1 * pxo.L1Norm((N)), K=D) x0, z0 = np.zeros((2, N)) cv.fit(x0=x0, z0=z0) x_recons = cv.solution() plt.figure() plt.stem(x, linefmt="C0-", markerfmt="C0o") mask_ids = np.where(downsample.adjoint(np.ones_like(y)))[0] markerline, stemlines, baseline = plt.stem(mask_ids, y, linefmt="C3-", markerfmt="C3o") markerline.set_markerfacecolor("none") plt.stem(x_recons, linefmt="C1--", markerfmt="C1s") plt.legend(["Ground truth", "Observation", "CV Estimate"]) plt.show()
(
Source code,png,hires.png,pdf)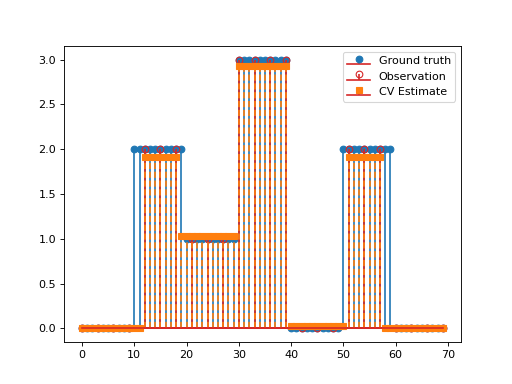
See also
- class PD3O(f=None, g=None, h=None, K=None, **kwargs)[source]#
Bases:
_PrimalDualSplittingPrimal-Dual Three-Operator Splitting (PD3O) algorithm.
The Primal-Dual three Operator splitting (PD3O) method is described in [PD3O].
It can be used to solve problems of the form:
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\Psi(\mathbf{x}):=\mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{G}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathcal{K} \mathbf{x}),}\]where:
\(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).
\(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) and \(\mathcal{H}:\mathbb{R}^M\rightarrow \mathbb{R}\cup\{+\infty\}\) are proper, lower semicontinuous and convex functions with simple proximal operators.
\(\mathcal{K}:\mathbb{R}^N\rightarrow \mathbb{R}^M\) is a differentiable map (e.g. a linear operator \(\mathbf{K}\)), with operator norm:
\[\Vert{\mathcal{K}}\Vert_2=\sup_{\mathbf{x}\in\mathbb{R}^N,\Vert\mathbf{x}\Vert_2=1} \Vert\mathcal{K}(\mathbf{x})\Vert_2.\]
Remarks#
The problem is feasible – i.e. there exists at least one solution.
The algorithm is still valid if one or more of the terms \(\mathcal{F}\), \(\mathcal{G}\) or \(\mathcal{H}\) is zero.
The algorithm has convergence guarantees for the case in which \(\mathcal{H}\) is composed with a linear operator \(\mathbf{K}\). When \(\mathcal{F}=0\), convergence can be proven for non-linear differentiable maps \(\mathcal{K}\). (See [NLCP].) Note that this class does not yet support automatic selection of hyperparameters for the case of non-linear differentiable maps \(\mathcal{K}\).
Assume that the following holds:
\(\gamma\geq\frac{\beta}{2}\),
\(\tau \in ]0, \frac{1}{\gamma}[\),
\(\tau\sigma\Vert\mathbf{K}\Vert_{2}^2 \leq 1\),
\(\delta = 2-\beta\tau/2 \in [1, 2[\) and \(\rho \in (0, \delta]\).
Then there exists a pair \((\mathbf{x}^\star,\mathbf{z}^\star)\in\mathbb{R}^N\times \mathbb{R}^M\) solution s.t. the primal and dual sequences of estimates \((\mathbf{x}_n)_{n\in\mathbb{N}}\) and \((\mathbf{z}_n)_{n\in\mathbb{N}}\) converge towards \(\mathbf{x}^\star\) and \(\mathbf{z}^\star\) respectively (Theorem 8.2 of [PSA]), i.e.
\[\lim_{n\rightarrow +\infty}\Vert\mathbf{x}^\star-\mathbf{x}_n\Vert_2=0, \quad \text{and} \quad \lim_{n\rightarrow +\infty}\Vert\mathbf{z}^\star-\mathbf{z}_n\Vert_2=0.\]Futhermore, when \(\rho=1\), the objective functional sequence \(\left(\Psi(\mathbf{x}_n)\right)_{n\in\mathbb{N}}\) can be shown to converge towards its minimum \(\Psi^\ast\) with rate \(o(1/\sqrt{n})\) (Theorem 1 of [dPSA]):
\[\Psi(\mathbf{x}_n) - \Psi^\ast = o(1/\sqrt{n}).\]
Parameters (
__init__())#Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.z0 (
NDArray,None) – (…, M) initial point(s) for the dual variable. IfNone(default), then useK(x0)as the initial point for the dual variable.beta (
Real,None) – Lipschitz constant \(\beta\) of \(\nabla\mathcal{F}\). If not provided, it will be automatically estimated.tuning_strategy (1, 2, 3) – Strategy to be employed when setting the hyperparameters (default to 1). See section below for more details.
**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
Default hyperparameter values
This class supports three strategies to automatically set the hyperparameters (see [PSA] for more details and numerical experiments comparing the performance of the three strategies):
tuning_strategy == 1: \(\gamma = \beta\) (safe step sizes) and \(\rho=1\) (no relaxation).This is the most standard way of setting the parameters in the literature.
tuning_strategy == 2: \(\gamma = \beta/1.9\) (large step sizes) and \(\rho=1\) (no relaxation).This strategy favours large step sizes forbidding the use of overrelaxation. When \(\beta=0\), coincides with the first strategy.
tuning_strategy == 3: \(\gamma = \beta\) (safe step sizes) and \(\rho=\delta - 0.1 > 1\) (overrelaxation).This strategy chooses smaller step sizes, but performs overrelaxation.
Once \(\gamma\) chosen, the convergence speed of the algorithm is improved by choosing \(\sigma\) and \(\tau\) as large as possible and relatively well-balanced – so that both the primal and dual variables converge at the same pace. Whenever possible, we therefore choose perfectly balanced parameters \(\sigma=\tau\) saturating the convergence inequalities for a given value of \(\gamma\).
In practice, the following linear programming optimization problem is solved:
\[\begin{split}(\tau, \, \sigma) = \operatorname{arg} \max_{(\tau^{*}, \, \sigma^{*})} \quad & \operatorname{log}(\tau^{*}) + \operatorname{log}(\sigma^{*})\\ \text{s.t.} \quad & \operatorname{log}(\tau^{*}) + \operatorname{log}(\sigma^{*}) \leq 2\operatorname{log}(\Vert\mathbf{K}\Vert_{2})\\ & \operatorname{log}(\tau^{*}) \leq -\operatorname{log}(\gamma)\\ & \operatorname{log}(\tau^{*}) = \operatorname{log}(\sigma^{*}).\end{split}\]When \(\tau \leq 1/\gamma\) is given (i.e., \(\tau=\tau_{1}\)), but not \(\sigma\), the latter is chosen as:
\[\tau_{1}\sigma\Vert\mathbf{K}\Vert_{2}^2= 1 \quad\Longleftrightarrow\quad \sigma=\frac{1}{\tau_{1}\Vert\mathbf{K}\Vert_{2}^{2}}.\]When \(\sigma\) is given (i.e., \(\sigma=\sigma_{1}\)), but not \(\tau\), the latter is chosen as:
\[\tau = \min \left\{\frac{1}{\gamma}, \frac{1}{\sigma_{1}\Vert\mathbf{K}\Vert_{2}^{2}}\right\}.\]Warning
When values are provided for both \(\tau\) and \(\sigma\), it is assumed that the latter satisfy the convergence inequalities, but no check is explicitly performed. Automatic selection of hyperparameters for the case of non-linear differentiable maps \(\mathcal{K}\) is not supported yet.
Example
Consider the following optimisation problem:
\[\min_{\mathbf{x}\in\mathbb{R}_+^N}\frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\quad+\quad\lambda_1 \|\mathbf{D}\mathbf{x}\|_1\quad+\quad\lambda_2 \|\mathbf{x}\|_1,\]with \(\mathbf{D}\in\mathbb{R}^{N\times N}\) the discrete derivative operator and \(\mathbf{G}\in\mathbb{R}^{L\times N}, \, \mathbf{y}\in\mathbb{R}^L, \lambda_1,\lambda_2>0.\) This problem can be solved via PD3O with \(\mathcal{F}(\mathbf{x})= \frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\), \(\mathcal{G}(\mathbf{x})=\lambda_2\|\mathbf{x}\|_1,\) \(\mathcal{H}(\mathbf{x})=\lambda \|\mathbf{x}\|_1\) and \(\mathbf{K}=\mathbf{D}\).
import matplotlib.pyplot as plt import numpy as np import pyxu.operator as pxo from pyxu.operator import SubSample, PartialDerivative from pyxu.opt.solver import PD3O x = np.repeat(np.asarray([0, 2, 1, 3, 0, 2, 0]), 10) N = x.size D = PartialDerivative.finite_difference(dim_shape=(N,), order=(1,)) downsample = SubSample(N, slice(None, None, 3)) y = downsample(x) loss = (1 / 2) * pxo.SquaredL2Norm(y.size).argshift(-y) F = loss * downsample pd3o = PD3O(f=F, g=0.01 * pxo.L1Norm(N), h=0.1 * pxo.L1Norm((N)), K=D) x0, z0 = np.zeros((2, N)) pd3o.fit(x0=x0, z0=z0) x_recons = pd3o.solution() plt.figure() plt.stem(x, linefmt="C0-", markerfmt="C0o") mask_ids = np.where(downsample.adjoint(np.ones_like(y)))[0] markerline, stemlines, baseline = plt.stem(mask_ids, y, linefmt="C3-", markerfmt="C3o") markerline.set_markerfacecolor("none") plt.stem(x_recons, linefmt="C1--", markerfmt="C1s") plt.legend(["Ground truth", "Observation", "PD3O Estimate"]) plt.show()
(
Source code,png,hires.png,pdf)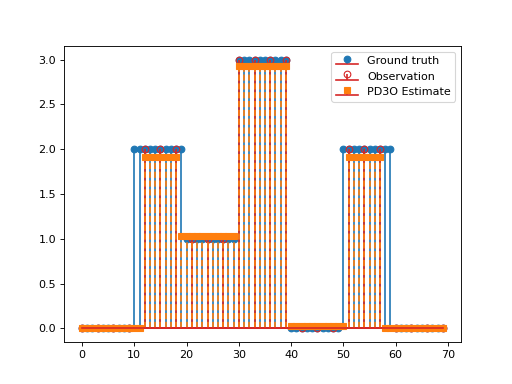
- ChambollePock(g=None, h=None, K=None, base=<class 'pyxu.opt.solver.pds.CondatVu'>, **kwargs)[source]#
Chambolle-Pock primal-dual splitting method.
- Parameters:
The Chambolle-Pock (CP) primal-dual splitting method can be used to solve problems of the form:
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \mathcal{G}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathbf{K} \mathbf{x}),}\]where:
\(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) and \(\mathcal{H}:\mathbb{R}^M\rightarrow \mathbb{R}\cup\{+\infty\}\) are proper, lower semicontinuous and convex functions with simple proximal operators.
\(\mathcal{K}:\mathbb{R}^N\rightarrow \mathbb{R}^M\) is a differentiable map (e.g. a linear operator \(\mathbf{K}\)), with operator norm:
\[\Vert{\mathcal{K}}\Vert_2=\sup_{\mathbf{x}\in\mathbb{R}^N,\Vert\mathbf{x}\Vert_2=1} \Vert\mathcal{K}(\mathbf{x})\Vert_2.\]
Remarks#
The problem is feasible, i.e. there exists at least one solution.
The algorithm is still valid if one of the terms \(\mathcal{G}\) or \(\mathcal{H}\) is zero.
Automatic selection of parameters is not supported for non-linear differentiable maps \(\mathcal{K}\).
The Chambolle-Pock (CP) primal-dual splitting method can be obtained by choosing \(\mathcal{F}=0\) in
CondatVuorPD3O. Chambolle and Pock originally introduced the algorithm without relaxation (\(\rho=1\)) [CPA]. Relaxed versions have been proposed afterwards [PSA]. Chambolle-Pock’s algorithm is also known as the Primal-Dual Hybrid Gradient (PDHG) algorithm. It can be seen as a preconditionned ADMM method [CPA].
Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.z0 (
NDArray,None) – (…, M) initial point(s) for the dual variable. IfNone(default), then useK(x0)as the initial point for the dual variable.tuning_strategy (1, 2, 3) – Strategy to be employed when setting the hyperparameters (default to 1). See
basefor more details.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
See also
- CP(g=None, h=None, K=None, base=<class 'pyxu.opt.solver.pds.CondatVu'>, **kwargs)#
Alias of
ChambollePock().
- class LorisVerhoeven(f=None, h=None, K=None, **kwargs)[source]#
Bases:
PD3OLoris-Verhoeven splitting algorithm.
This solver is also accessible via the alias
LV.The Loris-Verhoeven (LV) primal-dual splitting can be used to solve problems of the form:
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathbf{K} \mathbf{x}),}\]where:
\(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).
\(\mathcal{H}:\mathbb{R}^M\rightarrow \mathbb{R}\cup\{+\infty\}\) is a proper, lower semicontinuous and convex function with simple proximal operator.
\(\mathcal{K}:\mathbb{R}^N\rightarrow \mathbb{R}^M\) is a differentiable map (e.g. a linear operator \(\mathbf{K}\)), with operator norm:
\[\Vert{\mathcal{K}}\Vert_2=\sup_{\mathbf{x}\in\mathbb{R}^N,\Vert\mathbf{x}\Vert_2=1} \Vert\mathcal{K}(\mathbf{x})\Vert_2.\]
Remarks#
The problem is feasible, i.e. there exists at least one solution.
The algorithm is still valid if one of the terms \(\mathcal{F}\) or \(\mathcal{H}\) is zero.
Automatic selection of parameters is not supported for non-linear differentiable maps \(\mathcal{K}\).
The Loris-Verhoeven (CP) primal-dual splitting method can be obtained by choosing \(\mathcal{G}=0\) in
PD3O.In the specific case where \(\mathcal{F}\) is quadratic, then one can set \(\rho \in ]0,\delta[\) with \(\delta=2\). (See Theorem 4.3 in [PSA].)
Parameters (
__init__())#f (
DiffFunc,None) – Differentiable function \(\mathcal{F}\).K (
DiffMap,LinOp,None) – Differentiable map or linear operator \(\mathcal{K}\).beta (
Real,None) – Lipschitz constant \(\beta\) of \(\nabla\mathcal{F}\). If not provided, it will be automatically estimated.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.__init__().
Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.z0 (
NDArray,None) – (…, M) initial point(s) for the dual variable. IfNone(default), then useK(x0)as the initial point for the dual variable.tuning_strategy (1, 2, 3) – Strategy to be employed when setting the hyperparameters (default to 1). See
PD3Ofor more details.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
See also
- LV#
alias of
LorisVerhoeven
- class DavisYin(f, g=None, h=None, **kwargs)[source]#
Bases:
PD3ODavis-Yin primal-dual splitting method.
This solver is also accessible via the alias
DY.The Davis-Yin (DY) primal-dual splitting method can be used to solve problems of the form:
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{G}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathbf{x}),}\]where:
\(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).
\(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) and \(\mathcal{H}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) are proper, lower semicontinuous and convex functions with simple proximal operators.
Remarks#
The problem is feasible, i.e. there exists at least one solution.
The algorithm is still valid if one of the terms \(\mathcal{G}\) or \(\mathcal{H}\) is zero.
The Davis-Yin primal-dual splitting method can be obtained by choosing \(\mathcal{K}=\mathbf{I}\) (identity) and \(\tau=1/\sigma\) in
PD3O, provided a suitable change of variable [PSA].
Parameters (
__init__())#f (
DiffFunc) – Differentiable function \(\mathcal{F}\).beta (
Real,None) – Lipschitz constant \(\beta\) of \(\nabla\mathcal{F}\). If not provided, it will be automatically estimated.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.__init__().
Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.z0 (
NDArray,None) – (…, N) initial point(s) for the dual variable. IfNone(default), then usex0as the initial point for the dual variable.tuning_strategy (1, 2, 3) – Strategy to be employed when setting the hyperparameters (default to 1). See
PD3Ofor more details.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
See also
PD3O,LorisVerhoeven,PGD,ChambollePock(),DouglasRachford()
- DouglasRachford(g=None, h=None, base=<class 'pyxu.opt.solver.pds.CondatVu'>, **kwargs)[source]#
Douglas-Rachford splitting algorithm.
- Parameters:
The Douglas-Rachford (DR) primal-dual splitting method can be used to solve problems of the form:
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \mathcal{G}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathbf{x}),}\]where \(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) and \(\mathcal{H}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) are proper, lower semicontinuous and convex functions with simple proximal operators.
Remarks#
The problem is feasible, i.e. there exists at least one solution.
The algorithm is still valid if one of the terms \(\mathcal{G}\) or \(\mathcal{H}\) is zero.
The Douglas-Rachford (DR) primal-dual splitting method can be obtained by choosing \(\mathcal{F}=0\), \(\mathbf{K}=\mathbf{Id}\) and \(\tau=1/\sigma\) in
CondatVuorPD3O. Douglas and Rachford originally introduced the algorithm without relaxation (\(\rho=1\)), but relaxed versions have been proposed afterwards [PSA]. When \(\rho=1\), Douglas-Rachford’s algorithm is functionally equivalent to ADMM (up to a change of variable, see [PSA] for a derivation).
Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.z0 (
NDArray,None) – (…, N) initial point(s) for the dual variable. IfNone(default), then usex0as the initial point for the dual variable.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
See also
- DR(g=None, h=None, base=<class 'pyxu.opt.solver.pds.CondatVu'>, **kwargs)#
Alias of
DouglasRachford().
- class ForwardBackward(f=None, g=None, **kwargs)[source]#
Bases:
CondatVuForward-backward splitting algorithm.
This solver is also accessible via the alias
FB.The Forward-backward (FB) splitting method can be used to solve problems of the form:
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{G}(\mathbf{x}),}\]where:
\(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).
\(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) is proper, lower semicontinuous and convex function with simple proximal operator.
Remarks#
The problem is feasible, i.e. there exists at least one solution.
The algorithm is still valid if one of the terms \(\mathcal{F}\) or \(\mathcal{G}\) is zero.
The Forward-backward (FB) primal-dual splitting method can be obtained by choosing \(\mathcal{H}=0\) in
CondatVu. Mercier originally introduced the algorithm without relaxation (\(\rho=1\)) [FB]. Relaxed versions have been proposed afterwards [PSA]. The Forward-backward algorithm is also known as the Proximal Gradient Descent (PGD) algorithm. For the accelerated version of PGD, usePGD.
Parameters (
__init__())#Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.z0 (
NDArray,None) – (…, N) initial point(s) for the dual variable. IfNone(default), then usex0as the initial point for the dual variable.tuning_strategy (1, 2, 3) – Strategy to be employed when setting the hyperparameters (default to 1). See
CondatVufor more details.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
See also
- FB#
alias of
ForwardBackward
- ProximalPoint(g=None, base=<class 'pyxu.opt.solver.pds.CondatVu'>, **kwargs)[source]#
Proximal-point method.
- Parameters:
The Proximal-point (PP) method can be used to solve problems of the form:
\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\mathcal{G}(\mathbf{x}),}\]where \(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) is proper, lower semicontinuous and convex function with simple proximal operator.
Remarks#
The problem is feasible, i.e. there exists at least one solution.
The Proximal-point algorithm can be obtained by choosing \(\mathcal{F}=0\) and \(\mathcal{H}=0\) in
CondatVuorPD3O. The original version of the algorithm was introduced without relaxation (\(\rho=1\)) [PP]. Relaxed versions have been proposed afterwards [PSA].
Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
See also
- PP(g=None, base=<class 'pyxu.opt.solver.pds.CondatVu'>, **kwargs)#
Alias of
ProximalPoint().- Parameters:
g (ProxFunc | None)
base (_PrimalDualSplitting | None)
- class ADMM(f=None, h=None, K=None, solver=None, solver_kwargs=None, **kwargs)[source]#
Bases:
_PrimalDualSplittingAlternating Direction Method of Multipliers.
The Alternating Direction Method of Multipliers (ADMM) can be used to solve problems of the form:
\[\min_{\mathbf{x}\in\mathbb{R}^N} \quad \mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathbf{K}\mathbf{x}),\]where (see below for additional details on the assumptions):
\(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) is a proper, lower semicontinuous and convex functional potentially with simple proximal operator or Lipschitz-differentiable,
\(\mathcal{H}:\mathbb{R}^M\rightarrow \mathbb{R}\cup\{+\infty\}\) is a proper, lower semicontinuous and convex functional with simple proximal operator,
\(\mathbf{K}:\mathbb{R}^N\rightarrow \mathbb{R}^M\) is a linear operator with operator norm \(\Vert{\mathbf{K}}\Vert_2\).
Remarks#
The problem is feasible, i.e. there exists at least one solution.
The algorithm is still valid if either \(\mathcal{F}\) or \(\mathcal{H}\) is zero.
When \(\mathbf{K} = \mathbf{I}_{N}\), ADMM is equivalent to the
DouglasRachford()method (up to a change of variable, see [PSA] for a derivation).This is an implementation of the algorithm described in Section 5.4 of [PSA], which handles the non-smooth composite term \(\mathcal{H}(\mathbf{K}\mathbf{x})\) by means of a change of variable and an infimal postcomposition trick. The update equation of this algorithm involves the following \(\mathbf{x}\)-minimization step:
(1)#\[\mathcal{V} = \operatorname*{arg\,min}_{\mathbf{x} \in \mathbb{R}^N} \quad \mathcal{F}(\mathbf{x}) + \frac1{2 \tau} \Vert \mathbf{K} \mathbf{x} - \mathbf{a} \Vert_2^2,\]where \(\tau\) is the primal step size and \(\mathbf{a} \in \mathbb{R}^M\) is an iteration-dependant vector.
The following cases are covered in this implementation:
\(\mathbf{K}\) is
None(i.e. the identity operator) and \(\mathcal{F}\) is aProxFunc. Then, (1) has a single solution provided by \(\operatorname*{prox}_{\tau \mathcal{F}}(\mathbf{a})\). This yields the classical ADMM algorithm described in Section 5.3 of [PSA] (i.e. without the postcomposition trick).\(\mathcal{F}\) is a
QuadraticFunc, i.e. \(\mathcal{F}(\mathbf{x})=\frac{1}{2} \langle\mathbf{x}, \mathbf{Q}\mathbf{x}\rangle + \mathbf{c}^T\mathbf{x} + t\). Then the unique solution to (1) is obtained by solving a linear system of the form:(2)#\[\Big( \mathbf{Q} + \frac1\tau \mathbf{K}^* \mathbf{K} \Big) \mathbf{x} = \frac1\tau \mathbf{K}^\ast\mathbf{a}-\mathbf{c}, \qquad \mathbf{x} \in \mathbb{R}^N.\]This linear system is solved via a sub-iterative
CGalgorithm involving the repeated application of \(\mathbf{Q}\) and \(\mathbf{K}^{*}\mathbf{K}\). This sub-iterative scheme may be computationally intensive if these operators do not admit fast matrix-free implementations.\(\mathcal{F}\) is a
DiffFunc. Then, (1) is solved via a sub-iterativeNLCGalgorithm involving repeated evaluation of \(\nabla\mathcal{F}\) and \(\mathbf{K}^{*}\mathbf{K}\). This sub-iterative scheme may be costly if these operators cannot be evaluated with fast algorithms. In this scenario, the use of multiple initial points infit()is not supported.
The user may also provide a custom callable solver \(s: \mathbb{R}^M \times \mathbb{R} \to \mathbb{R}^N\), taking as input \((\mathbf{a}, \tau)\) and solving (1), i.e. \(s(\mathbf{a}, \tau) \in \mathcal{V}\). (See example below.) If
ADMMis initialized with such a solver, then the latter is used to solve (1) regardless of whether one of the above-mentioned cases is met.Unlike traditional implementations of ADMM,
ADMMsupports relaxation, i.e. \(\rho\neq 1\).
Parameters (
__init__())#f (
DiffFunc,ProxFunc,None) – Differentiable or proximable function \(\mathcal{F}\).solver (
Callable,None) – Custom callable to solve the \(\mathbf{x}\)-minimization step (1).If provided,
solvermust have the NumPy signature(n), (1) -> (n).solver_kwargs (
Mapping) – Keyword parameters passed to the__init__()method of sub-iterativeCGorNLCGsolvers.solver_kwargsis ignored ifsolverprovided.**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.__init__().
Parameters (
fit())#x0 (
NDArray) – (…, N) initial point(s) for the primal variable.z0 (
NDArray,None) – (…, M) initial point(s) for the dual variable. IfNone(default), then useK(x0)as the initial point for the dual variable.tuning_strategy (1, 2, 3) – Strategy to be employed when setting the hyperparameters (default to 1). See base class for more details.
solver_kwargs (
Mapping) – Keyword parameters passed to thefit()method of sub-iterativeCGorNLCGsolvers.solver_kwargsis ignored ifsolverwas provided in__init__().**kwargs (
Mapping) – Other keyword parameters passed on topyxu.abc.Solver.fit().
Warning
tuning_strategydocstring says to look at base class for details, but nothing mentioned there!Example
Consider the following optimization problem:
\[\min_{\mathbf{x}\in\mathbb{R}^N}\frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\quad+\quad\lambda \|\mathbf{D}\mathbf{x}\|_1,\]with \(\mathbf{D}\in\mathbb{R}^{N\times N}\) the discrete second-order derivative operator, \(\mathbf{G}\in\mathbb{R}^{M\times N}, \, \mathbf{y}\in\mathbb{R}^M, \lambda>0.\) This problem can be solved via ADMM with \(\mathcal{F}(\mathbf{x})= \frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\), \(\mathcal{H}(\mathbf{x})=\lambda \|\mathbf{D}\mathbf{x}\|_1,\) and \(\mathbf{K}=\mathbf{D}\). The functional \(\mathcal{F}\) being quadratic, the \(\mathbf{x}\)-minimization step consists in solving a linear system of the form (2). Here, we demonstrate how to provide a custom solver, which consists in applying a matrix inverse, for this step. Otherwise, a sub-iterative
CGalgorithm would have been used automatically instead.import matplotlib.pyplot as plt import numpy as np import pyxu.abc as pxa import pyxu.operator as pxo import scipy as sp from pyxu.opt.solver import ADMM N = 100 # Dimension of the problem # Generate piecewise-linear ground truth x_gt = np.array([10, 25, 60, 90]) # Knot locations a_gt = np.array([2, -4, 3, -2]) # Amplitudes of the knots gt = np.zeros(N) # Ground-truth signal for n in range(len(x_gt)): gt[x_gt[n] :] += a_gt[n] * np.arange(N - x_gt[n]) / N # Generate data (noisy samples at random locations) M = 20 # Number of data points rng = np.random.default_rng(seed=0) x_samp = rng.choice(np.arange(N // M), size=M) + np.arange(N, step=N // M) # sampling locations sigma = 2 * 1e-2 # noise variance y = gt[x_samp] + sigma * rng.standard_normal(size=M) # noisy data points # Data-fidelity term subsamp_mat = sp.sparse.lil_matrix((M, N)) for i in range(M): subsamp_mat[i, x_samp[i]] = 1 G = pxa.LinOp.from_array(subsamp_mat.tocsr()) F = 1 / 2 * pxo.SquaredL2Norm(dim=y.size).argshift(-y) * G F.diff_lipschitz = F.estimate_diff_lipschitz(method="svd") # Regularization term (promotes sparse second derivatives) deriv_mat = sp.sparse.diags(diagonals=[1, -2, 1], offsets=[0, 1, 2], shape=(N - 2, N)) D = pxa.LinOp.from_array(deriv_mat) _lambda = 1e-1 # regularization parameter H = _lambda * pxo.L1Norm(dim=D.codim) # Solver for ADMM tau = 1 / _lambda # internal ADMM parameter # Inverse operator to solve the linear system A_inv = sp.linalg.inv(G.gram().asarray() + (1 / tau) * D.gram().asarray()) def solver_ADMM(arr, tau): b = (1 / tau) * D.adjoint(arr) + G.adjoint(y) return A_inv @ b.squeeze() # Solve optimization problem admm = ADMM(f=F, h=H, K=D, solver=solver_ADMM,show_progress=False) # with solver admm.fit(x0=np.zeros(N), tau=tau) x_opt = admm.solution() # reconstructed signal # Plots plt.figure() plt.plot(np.arange(N), gt, label="Ground truth") plt.plot(x_samp, y, "kx", label="Noisy data points") plt.plot(np.arange(N), x_opt, label="Reconstructed signal") plt.legend()
See also