pyxu.util#

pyxu.util.array_module#

get_array_module(x, fallback=None)[source]#

Get the array namespace corresponding to a given object.

Parameters:

  • x (object) – Any object compatible with the interface of NumPy arrays.

  • fallback (ArrayModule) – Fallback module if x is not a NumPy-like array. Default behaviour: raise error if fallback used.

Returns:

namespace – The namespace to use to manipulate x, or fallback if provided.

Return type:

ArrayModule

redirect(i, **kwargs)[source]#

Change codepath for supplied array backends.

Some functions/methods cannot be written in module-agnostic fashion. The action of this decorator is summarized below:

  • Analyze an array-valued parameter (x) of the wrapped function/method (f).

  • If x lies in one of the supplied array namespaces: re-route execution to the specified function.

  • If x lies in none of the supplied array namespaces: execute f.

Parameters:
Return type:

Callable

Notes

Auto-dispatch via redirect() assumes the dispatcher/dispatchee have the same parameterization, i.e.:

  • if f is a function -> dispatch possible to another callable with identical signature (i.e., function or staticmethod)

  • if f is a staticmethod -> dispatch possible to another callable with identical signature (i.e., function or staticmethod)

  • if f is an instance-method -> dispatch to another instance-method of the class with identical signature.

Example

def f(x, y): return "f"

@redirect('x', NUMPY=f)    # if 'x' is of type NDArrayInfo.NUMPY, i.e. has
def g(x, y): return "g"    # short-name 'NUMPY' -> reroute execution to `f`

x1 = np.arange(5)
x2 = da.array(x1)
y = 1
g(x1, y), g(x2, y)  # 'f', 'g'
compute(*args, mode='compute', **kwargs)[source]#

Force computation of Dask collections.

Parameters:

  • *args (object, list) – Any number of objects. If it is a dask object, it is evaluated and the result is returned. Non-dask arguments are passed through unchanged. Python collections are traversed to find/evaluate dask objects within. (Use traverse =False to disable this behavior.)

  • mode (str) – Dask evaluation strategy: compute or persist.

  • **kwargs (dict) – Extra keyword parameters forwarded to dask.compute() or dask.persist().

Returns:

*cargs – Evaluated objects. Non-dask arguments are passed through unchanged.

Return type:

object, list

to_NUMPY(x)[source]#

Convert an array from a specific backend to NUMPY.

Parameters:

x (NDArray) – Array to be converted.

Returns:

y – Array with NumPy backend.

Return type:

NDArray

Notes

This function is a no-op if the array is already a NumPy array.

pyxu.util.complex#

as_real_op(A, dim_rank=None)[source]#

View complex-valued linear operator as its real-valued equivalent.

Useful to transform complex-valued matrix/vector products to their real-valued counterparts.

Parameters:

  • A (NDArray) – (N1…,NK, M1,…,MD) complex-valued matrix.

  • dim_rank (Integer) – Dimension rank \(D\). (Can be omitted if A is 2D.)

Returns:

A_r – (N1,…,NK,2, M1,…,MD,2) real-valued equivalent.

Return type:

NDArray

Examples

import numpy as np
import pyxu.util.complex as cpl

codim_shape = (1,2,3)
dim_shape = (4,5,6,7)
dim_rank = len(dim_shape)

rng = np.random.default_rng(0)
A =      rng.standard_normal((*codim_shape, *dim_shape)) \
  + 1j * rng.standard_normal((*codim_shape, *dim_shape))    # (1,2,3  |4,5,6,7  )
A_r = cpl.as_real_op(A, dim_rank=dim_rank)                  # (1,2,3,2|4,5,6,7,2)

x =      rng.standard_normal(dim_shape) \
  + 1j * rng.standard_normal(dim_shape)                     # (4,5,6,7  )
x_r = cpl.view_as_real(x)                                   # (4,5,6,7,2)

y = np.tensordot(A, x, axes=dim_rank)                       # (1,2,3  )
y_r = np.tensordot(A_r, x_r, axes=dim_rank+1)               # (1,2,3,2)

np.allclose(y, cpl.view_as_complex(y_r))                    # True

Notes

Real-valued matrices are returned unchanged.

See also

view_as_real(), view_as_complex()

require_viewable(x)[source]#

Copy array if required to do real/complex view manipulations.

Real/complex view manipulations are feasible if the last axis is contiguous.

Parameters:

x (NDArray)

Returns:

y

Return type:

NDArray

view_as_complex(x)[source]#

View real-valued array as its complex-valued bijection. (Inverse of view_as_real().)

Parameters:

x (NDArray) – (…, N, 2) real-valued array.

Returns:

y – (…, N) complex-valued array.

Return type:

NDArray

Examples

from pyxu.util import view_as_real, view_as_complex
x = np.array([[0., 1],
              [2 , 3],
              [4 , 5]])
y = view_as_complex(x)  # array([0.+1.j, 2.+3.j, 4.+5.j])
view_as_real(y) == x    # True

Notes

Complex-valued inputs are returned unchanged.

See also

as_real_op(), view_as_real()

view_as_real(x)[source]#

View complex-valued array as its real-valued bijection. (Inverse of view_as_complex().)

Parameters:

x (NDArray) – (…, N) complex-valued array.

Returns:

y – (…, N, 2) real-valued array.

Return type:

NDArray

Examples

from pyxu.util import view_as_real, view_as_complex
x = np.r_[0+1j, 2+3j, 4+5j]
y = view_as_real(x)               # array([[0., 1.],
                                  #        [2., 3.],
                                  #        [4., 5.]])
view_as_complex(y) == x           # True

Notes

Real-valued inputs are returned unchanged.

See also

as_real_op(), view_as_complex()

pyxu.util.misc#

copy_if_unsafe(x)[source]#

Copy array if it is unsafe to do in-place updates on it.

In-place updates are unsafe if:

  • the array is read-only, OR

  • the array is a view onto another array.

Parameters:

x (NDArray)

Returns:

y

Return type:

NDArray

import_module(name, fail_on_error=True)[source]#

Load a Python module dynamically.

Parameters:
Return type:

ModuleType

parse_params(func, *args, **kwargs)[source]#

Get function parameterization.

Returns:

params – (key, value) params as seen in body of func when called via func(*args, **kwargs).

Return type:

Mapping

read_only(x)[source]#

Make an array read-only.

Parameters:

x (NDArray)

Returns:

y

Return type:

NDArray

peaks(x, y)[source]#

Matlab 2D peaks function.

Peaks is a function of two variables, obtained by translating and scaling Gaussian distributions. (See Matlab’s peaks function.)

This function is useful for testing purposes.

Parameters:
Returns:

z – Values of the 2D function peaks at the points specified by the entries of x and y.

Return type:

NDArray

Examples

import numpy as np
import matplotlib.pyplot as plt
from pyxu.util.misc import peaks

x = np.linspace(-3, 3, 1000)
xx, yy = np.meshgrid(x, x)
z = peaks(xx, yy)
plt.figure()
plt.imshow(z)

(Source code, png, hires.png, pdf)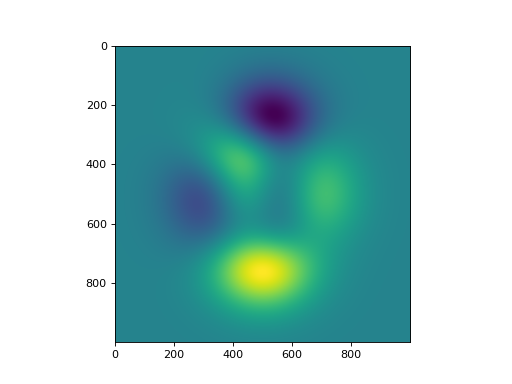

../_images/util-1.png
star_like_sample(N, w, s, po, x0, ndi=NDArrayInfo.NUMPY)[source]#

Star-like test image.

Generates a (N, N) square image of a star-like object normalized between 0 and 1. Based on GlobalBioIm’s StarLikeSample function. This function is useful for testing purposes as it contains high-frequency information.

Parameters:

  • N (Integer) – Size of the image (must be an even number).

  • w (Integer) – The number of branches of the sample will be 4*w.

  • s (Real) – Slope of the sigmoid function \(\frac1{1+\exp[s (x-x_{0})]}\) attenuating the boundaries.

  • po (Integer) – Power-raising factor for the final image (to have smoother edges).

  • x0 (Real) – Radial shift of the sigmoid function \(\frac1{1+\exp[s (x-x_{0})]}\).

  • ndi (NDArrayInfo) – Desired array module for the output.

Returns:

image – (N, N) image of star-like sample.

Return type:

NDArray

Examples

import numpy as np
import matplotlib.pyplot as plt
from pyxu.util.misc import star_like_sample

star = star_like_sample(N=256, w=8, s=20, po=3, x0=0.7)
plt.figure()
plt.imshow(star)

(Source code, png, hires.png, pdf)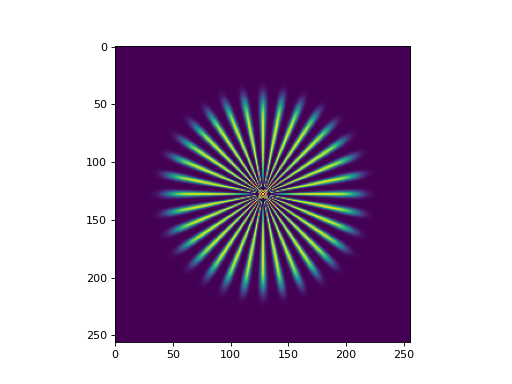

../_images/util-2.png

pyxu.util.operator#

as_canonical_axes(axes, rank)[source]#

Transform NDarray axes into tuple-form with positive indices.

Parameters:
Return type:

Integral | tuple[Integral, …]

as_canonical_shape(x)[source]#

Transform a lone integer into a valid tuple-based shape specifier.

Parameters:

x (Integral | tuple[Integral, ...])

Return type:

Integral | tuple[Integral, …]

vectorize(i, dim_shape, codim_shape)[source]#

Decorator to auto-vectorize a function \(\mathbf{f}: \mathbb{R}^{M_{1} \times\cdots\times M_{D}} \to \mathbb{R}^{N_{1} \times\cdots\times N_{K}}\) to accept stacking dimensions.

Parameters:

  • i (VarName) – Function/method parameter to vectorize. This variable must hold an object with a NumPy API.

  • dim_shape (NDArrayShape) – (M1,…,MD) shape of operator’s domain.

  • codim_shape (NDArrayShape) – (N1,…,NK) shape of operator’s co-domain.

Returns:

g – Function/Method with signature (..., M1,...,MD) -> (..., N1,...,NK) in parameter i.

Return type:

Callable

Example

import pyxu.util as pxu

def f(x):
    return x.sum(keepdims=True)

N = 5
g = pxu.vectorize("x", N, 1)(f)

x = np.arange(2*N).reshape((2, N))
g(x[0]), g(x[1])  #  [10], [35]
g(x)              #  [[10],
                  #   [35]]

Notes

  • vectorize() assumes the function being vectorized is thread-safe and can be evaluated in parallel. Using it on thread-unsafe code may lead to incorrect outputs.

  • As predicted by Pyxu’s Operator API:

    • The dtype of the vectorized function is assumed to match x.dtype.

    • The array backend of the vectorized function is assumed to match that of x.